يـعـتـمـد حـل نـظـام مـكـون مـن مـعـادلـتـيـن تـربـيـعـيـتـيـن عـلـى :
1 ـ حذف أحد المتغيرين .
2ـ إيجاد المتغير الآخر وتعويضه في المعادلة الأخرى لإيجاد قيمة المتغير الذي سبق حذفه .
مثال (1)
جد حلول النظام التالي :
2س2 + 3ص2 = 23 ……… معادلة 1
2س2 - ص2 = 7 ……… معادلة 2
الحل :
◘ الخطوة الأولى : نحذف احد المتغيرين وليكن المتغير (س2)
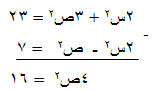
اقسم على 4 ينتج ص2 = 4 ==> ص = 2 ، - 2
◘ الخطوة الثانية : لإيجاد قيمة س نعوض قيم ص في إحدى المعادلتين مثلا المعادلة 1
* عندما ص = 2 فإنّ 2س2 + 3 (4) = 23 ==> 2س2 = 11 ==> س = ± 2.34
أي عندما ص = 2 هناك قيمتان لـ س
أي هناك حلان هما : (2.34 ، 2) ، (- 2.34 ، 2 )
* وعندما ص = - 2 فإنّ 2س2 + 3 (4) = 23 ==> س = ± 2.34
أي عندما ص = -2 هناك أيضا قيمتان لـ س :
أي هناك حلان هما : (2.34 ، -2) ، (- 2.34 ، -2 )
∴ للنظام أربعة حلول هي :
(2.34 ، 2) ، (- 2.34 ، 2 ) (2.34 ، -2) ، (- 2.34 ، -2 )
مثال (2)
جد حلّ نظام المعادلات التالية :
5س2 + ص2 = 36
س2 + 2 ص2 = 36
الحل :

ومنه ص2 = 4 ==> ص = 4 ، - 4
◘ والآن لإيجاد قيم س عوض في إحدى المعادلتين ولتكن المعادلة الأولى :
◘ عندما ص = 4 فإنّ 5 س2 + (4)2= 36 ==> س = 2 ، -2
∴ الأزواج المرتبة هي : (2 ، 4) ، (- 2 ، 4)
◘ وعندما ص = -4 فإنّ 5س2 + (-4)2 = 36 ==> س = 2 ، -2
∴ الأزواج المرتبة هي : (2 ، -4) ، (-2، -4)
أي هناك أربع حلول للنظام هي : (2 ، 4) ، ( -2 ، 4) ، (2 ، -4) (-2 ، -4)
مثال (3)
س2 + 3 ص2 = 7 ..…… معادلة (1)
2س2 - 3س ص + 4ص2 = 6 …….. معادلة (2)
الحل :
◘ لحل مثل هذا النظام (الذي يحتوي على س ص مع وجود متغيرات تربيعية س2 ، ص2)
نقوم بحذف الحد الثابت من المعادلتين
◘ احذف الحد الثابت وذلك بضرب المعادلة (1) في -6 والمعادلة (2) في 7
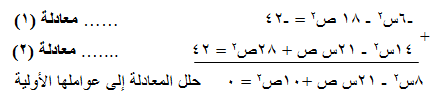
(8س - 5ص) ( س - 2ص) = 0
أما 8س - 5ص = 0 ….. معادلة 3
أو س - 2ص = 0 ….. معادلة 4
الآن انت حصلت على معادلات خطية ...
(خد المعادلة 1 مع المعادلة 3 وحل النظام ، ثم خذ المعادلة 1 مع المعادلة 4 وحل النظام)
◘ الآن خذ المعادلة (1) مع المعادلة (3) وحلّ النظام :
س2 + 3 ص2 = 7 …… معادلة 1
8س - 5ص = 0 …... معادلة 3
• اجعل ص بدلالة س في المعادلة الخطية (3) ==> ص = 8 / 5 س ==> ص = 1.6 س
• عوض ما حصلت عليه في المعادلة التربيعية (1) : س2 + 3 ص2 = 7
س2 + 3 × (1.6س)2 = 7 ==> س2 + 7.68 س2 = 7 ==> س = ± 0.898
• لتجد قيم ص عوض في المعادلة الخطية : ص = 1.6 س
∴ عندما س = 0.898 فإن ص = 1.6 × 0.898 ==> ص = 1.43
وعندما س = -0.898 فإن ص = 1.6 × -0.898 ==> ص = -1.43
إذن حصلنا على حلين هما : (0.898 ، 1.43) ، (-0.898 ، -1.43)
◘ والآن خذ المعادلة (1) مع المعادلة (4) وحلّ النظام :
س2 + 3 ص2 = 7 …… معادلة 1
س - 2ص = 0 ….. معادلة 4
• اجعل س بدلالة ص في المعادلة الخطية (4) ==> س = 2ص
• عوض ما حصلت عليه في المعادلة التربيعية (1) : س2 + 3 ص2 = 7
(2ص)2 + 3ص2 = 7 ==> 4ص2 + 3ص2 = 7 ==> ص = ±1
• لتجد قيم س عوض في المعادلة الخطية : س = 2ص
عندما ص = 1 ، فإن س = 2
وعندما ص = -1 فإن س = -2
إذن حصلنا على حلين أيضا هما : (2 ، 1) ، (-2 ، -1)
∴ حلول النظام هي : (0.898 ، 1.43) ، (-0.898 ، -1.43) (2 ، 1) ، (-2 ، -1)
منقول :. سلسبيل الخطيب
1 ـ حذف أحد المتغيرين .
2ـ إيجاد المتغير الآخر وتعويضه في المعادلة الأخرى لإيجاد قيمة المتغير الذي سبق حذفه .
مثال (1)
جد حلول النظام التالي :
2س2 + 3ص2 = 23 ……… معادلة 1
2س2 - ص2 = 7 ……… معادلة 2
الحل :
◘ الخطوة الأولى : نحذف احد المتغيرين وليكن المتغير (س2)
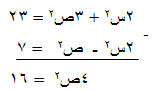
اقسم على 4 ينتج ص2 = 4 ==> ص = 2 ، - 2
◘ الخطوة الثانية : لإيجاد قيمة س نعوض قيم ص في إحدى المعادلتين مثلا المعادلة 1
* عندما ص = 2 فإنّ 2س2 + 3 (4) = 23 ==> 2س2 = 11 ==> س = ± 2.34
أي عندما ص = 2 هناك قيمتان لـ س
أي هناك حلان هما : (2.34 ، 2) ، (- 2.34 ، 2 )
* وعندما ص = - 2 فإنّ 2س2 + 3 (4) = 23 ==> س = ± 2.34
أي عندما ص = -2 هناك أيضا قيمتان لـ س :
أي هناك حلان هما : (2.34 ، -2) ، (- 2.34 ، -2 )
∴ للنظام أربعة حلول هي :
(2.34 ، 2) ، (- 2.34 ، 2 ) (2.34 ، -2) ، (- 2.34 ، -2 )
مثال (2)
جد حلّ نظام المعادلات التالية :
5س2 + ص2 = 36
س2 + 2 ص2 = 36
الحل :

ومنه ص2 = 4 ==> ص = 4 ، - 4
◘ والآن لإيجاد قيم س عوض في إحدى المعادلتين ولتكن المعادلة الأولى :
◘ عندما ص = 4 فإنّ 5 س2 + (4)2= 36 ==> س = 2 ، -2
∴ الأزواج المرتبة هي : (2 ، 4) ، (- 2 ، 4)
◘ وعندما ص = -4 فإنّ 5س2 + (-4)2 = 36 ==> س = 2 ، -2
∴ الأزواج المرتبة هي : (2 ، -4) ، (-2، -4)
أي هناك أربع حلول للنظام هي : (2 ، 4) ، ( -2 ، 4) ، (2 ، -4) (-2 ، -4)
مثال (3)
س2 + 3 ص2 = 7 ..…… معادلة (1)
2س2 - 3س ص + 4ص2 = 6 …….. معادلة (2)
الحل :
◘ لحل مثل هذا النظام (الذي يحتوي على س ص مع وجود متغيرات تربيعية س2 ، ص2)
نقوم بحذف الحد الثابت من المعادلتين
◘ احذف الحد الثابت وذلك بضرب المعادلة (1) في -6 والمعادلة (2) في 7
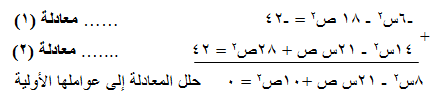
(8س - 5ص) ( س - 2ص) = 0
أما 8س - 5ص = 0 ….. معادلة 3
أو س - 2ص = 0 ….. معادلة 4
الآن انت حصلت على معادلات خطية ...
(خد المعادلة 1 مع المعادلة 3 وحل النظام ، ثم خذ المعادلة 1 مع المعادلة 4 وحل النظام)
◘ الآن خذ المعادلة (1) مع المعادلة (3) وحلّ النظام :
س2 + 3 ص2 = 7 …… معادلة 1
8س - 5ص = 0 …... معادلة 3
• اجعل ص بدلالة س في المعادلة الخطية (3) ==> ص = 8 / 5 س ==> ص = 1.6 س
• عوض ما حصلت عليه في المعادلة التربيعية (1) : س2 + 3 ص2 = 7
س2 + 3 × (1.6س)2 = 7 ==> س2 + 7.68 س2 = 7 ==> س = ± 0.898
• لتجد قيم ص عوض في المعادلة الخطية : ص = 1.6 س
∴ عندما س = 0.898 فإن ص = 1.6 × 0.898 ==> ص = 1.43
وعندما س = -0.898 فإن ص = 1.6 × -0.898 ==> ص = -1.43
إذن حصلنا على حلين هما : (0.898 ، 1.43) ، (-0.898 ، -1.43)
◘ والآن خذ المعادلة (1) مع المعادلة (4) وحلّ النظام :
س2 + 3 ص2 = 7 …… معادلة 1
س - 2ص = 0 ….. معادلة 4
• اجعل س بدلالة ص في المعادلة الخطية (4) ==> س = 2ص
• عوض ما حصلت عليه في المعادلة التربيعية (1) : س2 + 3 ص2 = 7
(2ص)2 + 3ص2 = 7 ==> 4ص2 + 3ص2 = 7 ==> ص = ±1
• لتجد قيم س عوض في المعادلة الخطية : س = 2ص
عندما ص = 1 ، فإن س = 2
وعندما ص = -1 فإن س = -2
إذن حصلنا على حلين أيضا هما : (2 ، 1) ، (-2 ، -1)
∴ حلول النظام هي : (0.898 ، 1.43) ، (-0.898 ، -1.43) (2 ، 1) ، (-2 ، -1)
منقول :. سلسبيل الخطيب
التعديل الأخير بواسطة المشرف: