همسآت شرقية
طاقم الادارة
نبدأ ..
1/ شرح القسمة المطولة ( سهلة وممتعة) :
هذه الطريقة ولكن أنتم اشرحوها على نمط هندل
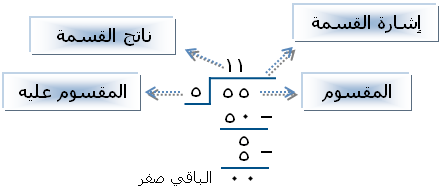
نأخذ أمثلة لنطبق عليها شرح الموضوع
المثال الأول : 494949\49
المثال الثاني : 1234\25
المثال الثالث : 432\36
قبل أن نبدأ بالقسمة المطولة علينا أن نعرف أنها تتكون من العمليات التالية بالترتيب
قسمة ===> ضرب ===> طرح ==> ودواليك
نبدأ بأول مثال
؟؟؟؟؟؟؟؟؟؟
494949|49
نبدأ بقسمة 4\49 ===> لا يمكن بالتأكيد ==> فنضع صفر في خانة خارج القسمة
؟؟؟؟؟؟؟؟؟0
494949|49
ونتابع بأخذ خانتين بدلا من خانة واحدة
؟؟؟؟؟؟؟؟؟0
494949|49
نقسم 49\49 = 1 ===> نضع واحد في خارج القسمة
ولكن تذكروا في بداية الموضوع اني قلت ان القسمة تحتوي على 3 عمليات
نحن قمنا باول عملية
العملية الثانية
الضرب
نضرب خارج القسمة الذي حصلنا عليه (1) في المقسوم عليه (49) والناتج نضعه تحت المقسوم (494949)
1×49 = 49 ===> نضعه تحت المقسوم , ثم نقوم بالعملية الأخيرة وهي الطرح
؟؟؟؟؟؟؟01
494949|49
؟؟؟؟؟؟؟49
؟؟؟؟؟؟؟00
نلاحظ اننا طرحنا اللي بالبني من اللي بالأحمر فكان الناتج صفر
الان ننتقل للخطوة التالية
نبدأ بأخذ الخانة الثالثة
004\49 ====> لا يمكن ===> نضع صفر في الناتج
؟؟؟؟؟؟010
494949|49
؟؟؟؟؟؟؟49
؟؟؟؟؟004
نأخذ الخانة الرابعة 0049\49 = 1
نضع واحد في الناتج ثم نقوم بالضرب ثم الطرح
؟؟؟؟0101
494949|49
؟؟؟؟؟49
؟؟0049
؟؟0049
؟؟0000
نتابع في الخطوة الاخير بنفس الطريقة
فيكون صورة القسمة كالتالي
010101
494949|49
؟؟؟؟؟؟؟49
؟؟؟؟0049
؟؟؟؟0049
000049
000049
000000
وبما أن الباقي في الأخير صفر
بكدة تكون انتهت القسمة
وان شاء الله تكون واضحة
494949|49
نبدأ بقسمة 4\49 ===> لا يمكن بالتأكيد ==> فنضع صفر في خانة خارج القسمة
؟؟؟؟؟؟؟؟؟0
494949|49
ونتابع بأخذ خانتين بدلا من خانة واحدة
؟؟؟؟؟؟؟؟؟0
494949|49
نقسم 49\49 = 1 ===> نضع واحد في خارج القسمة
ولكن تذكروا في بداية الموضوع اني قلت ان القسمة تحتوي على 3 عمليات
نحن قمنا باول عملية
العملية الثانية
الضرب
نضرب خارج القسمة الذي حصلنا عليه (1) في المقسوم عليه (49) والناتج نضعه تحت المقسوم (494949)
1×49 = 49 ===> نضعه تحت المقسوم , ثم نقوم بالعملية الأخيرة وهي الطرح
؟؟؟؟؟؟؟01
494949|49
؟؟؟؟؟؟؟49
؟؟؟؟؟؟؟00
نلاحظ اننا طرحنا اللي بالبني من اللي بالأحمر فكان الناتج صفر
الان ننتقل للخطوة التالية
نبدأ بأخذ الخانة الثالثة
004\49 ====> لا يمكن ===> نضع صفر في الناتج
؟؟؟؟؟؟010
494949|49
؟؟؟؟؟؟؟49
؟؟؟؟؟004
نأخذ الخانة الرابعة 0049\49 = 1
نضع واحد في الناتج ثم نقوم بالضرب ثم الطرح
؟؟؟؟0101
494949|49
؟؟؟؟؟49
؟؟0049
؟؟0049
؟؟0000
نتابع في الخطوة الاخير بنفس الطريقة
فيكون صورة القسمة كالتالي
010101
494949|49
؟؟؟؟؟؟؟49
؟؟؟؟0049
؟؟؟؟0049
000049
000049
000000
وبما أن الباقي في الأخير صفر
بكدة تكون انتهت القسمة
وان شاء الله تكون واضحة
الآن مع القسمة التي يحتوي خارج القسمة فيها على فواصل
1234\25
نقسم 1\25 ====> لا يمكن ===> نضع 0 في خارج القسمة ونتابع
نقسم 12\25 ===> لا يمكن ===> ايضا نضع صفر في خارج القسمة ونتابع
نقسم 123\25 = 4 ===> نضع 4 في خارج القسمة ثم نقوم بالضرب
4×25 = 100 === > نضع 100 تحت الـ(123) ثم نقوم بالطرح
123 - 100 = 23 ..
الآن نقوم بانزال 4 من المقسوم بجوار الـ(23)
فيتكون العدد 234 ==> نقسمه على 25
234\25 = 9
نقوم بالضرب 9×25 = 225
نضع 225 تحت 234 ونقوم بالطرح
234 - 225 = 9
يمكننا التوقف هنا ونقول ان الناتج 49 والباقي 9
او يمكننا الاكمال لايجاد الفاصلة العشرية
طبعا على حسب المطلوب في السؤال
الآن نكمل
بما ان 9\25 لا يمكن
ولم يعد هناك اعداد لننزلها من المقسوم
نضع فاصلة عشرية في خارج القسمة
ونضع صفر بجوار الـ(9)
ونستكمل القسمة
90\25=3
3×25 = 75
90 - 75 = 15
ننزل صفر آخر للـ(15) فتصبح 150
150\25= 6
نقوم بالضرب
6×25= 150
الطرح
150 - 150 = 0
بما ان الباقي صفر نكون خلصنا قسمة
ويكون الناتج النهائي هو 49.36
ان شاء الله تكون وااضحة ..
2/ إذا كان المقسوم عليه يحتوي على عدد يمكن ان نوصله إلى 10 أو أحد قوى العشرة
هذه الحالة تكون فقط عندما يكون المقسوم عليه مثلا 5 , 25 , 50 , 125 , ...
كما في المثال الثاني من الأمثلة التي لدينا
وهو
1234\25
هنا نلاحظ ان 25 يمكن ان نجعلها 100 بالضرب في 4
اذا نقوم بضرب البسط والمقام في 4
(1234×4)\(25×4) = 4936\100 = 49.36
نأخذ مثال آخر للتوضيح
605\50 = (605×2)\(50×2) = 1210\100 = 12.10
3/القسمة بالتبسيط :
أي نستمر في قسمة كل من البسط والمقام على عدد ما حتى نصل إلى أبسط صور لهذا الكسر
كما في المثال الثالث لدينا
432\36
نقسم كل من البسط والمقام على 2
216\18
نكرر العملية
108\9
نقسم كل من البسط والمقام على 3
36\3
نكرر العملية
12\1
وهو الناتج النهائي
4/ القسمة بالتقريب ====> تستعمل فقط مع الاسئلة الاختيارية
مثاال
100009\100
نلاحظ ان الـ(9) لن تؤثر كثيرا في الناتج النهائي
لذلك نطرحها من العدد
100009 - 9 = 100000
ونقوم بالقسمة الان
100000\100 = 1000
مع العلم ان الناتج الاصلي هو 1000.09
نلاحظ انه لا يوجد فرق كبير بينهما
5/طريقة تجزيء العدد إلى أعدد مجموعة لتسهيل القسمة أو الضرب :
وهي الطريقة التي أستعملها دائما
مثال
494949\49
العدد 494949 يمكن تقسيمه الى 490000 + 4900 + 49
الان نقوم بالقسمة
(490000 + 4900 + 49)\ 49
= (490000\49) + (4900\49) + (49\49)
= 10000 + 100 + 1 = 10101
ونلاحظ أنه نفس الناتج الذي حصلنا عليه بالقسمة المطولة ولكن بطريقة أسهل
مثال آخر
432\36
الان كيف نقسم العدد 432 الى أجزاء بحيث نسهل القسمة على 36
نضرب36 × 10 = 360
نطرح الـ(360) من الـ(432)
432 - 360 = 72
وبكذ نكون حصلنا على قسمين يسهل قسمتهم على 36
الان نقوم بالقسمة
(360 + 72)\36
=(360\36) + (72\36)
= 10 + 2 = 12
نلاحظ أنه نفس الناتج ولكن بطريقة أبسط بكثييير
الآن نأخذ مثال على الضرب
1234 × 4
نجزأ العدد 1234 الى
1000 + 200 + 30 + 4 ونقوم بالضرب
4×(1000 + 200 + 30 +4)
=(4×1000) + (4×200) + (4×30) + (4×4)
= 4000 + 800 + 120 + 16 = 4936
وصدقوني الطريقة الأخيرة دي مفييدة جدا وسهلت عليا القسمة والضرب كثيييرا
منقووووووووووووووول للفائدة
1234\25
نقسم 1\25 ====> لا يمكن ===> نضع 0 في خارج القسمة ونتابع
نقسم 12\25 ===> لا يمكن ===> ايضا نضع صفر في خارج القسمة ونتابع
نقسم 123\25 = 4 ===> نضع 4 في خارج القسمة ثم نقوم بالضرب
4×25 = 100 === > نضع 100 تحت الـ(123) ثم نقوم بالطرح
123 - 100 = 23 ..
الآن نقوم بانزال 4 من المقسوم بجوار الـ(23)
فيتكون العدد 234 ==> نقسمه على 25
234\25 = 9
نقوم بالضرب 9×25 = 225
نضع 225 تحت 234 ونقوم بالطرح
234 - 225 = 9
يمكننا التوقف هنا ونقول ان الناتج 49 والباقي 9
او يمكننا الاكمال لايجاد الفاصلة العشرية
طبعا على حسب المطلوب في السؤال
الآن نكمل
بما ان 9\25 لا يمكن
ولم يعد هناك اعداد لننزلها من المقسوم
نضع فاصلة عشرية في خارج القسمة
ونضع صفر بجوار الـ(9)
ونستكمل القسمة
90\25=3
3×25 = 75
90 - 75 = 15
ننزل صفر آخر للـ(15) فتصبح 150
150\25= 6
نقوم بالضرب
6×25= 150
الطرح
150 - 150 = 0
بما ان الباقي صفر نكون خلصنا قسمة
ويكون الناتج النهائي هو 49.36
ان شاء الله تكون وااضحة ..
2/ إذا كان المقسوم عليه يحتوي على عدد يمكن ان نوصله إلى 10 أو أحد قوى العشرة
هذه الحالة تكون فقط عندما يكون المقسوم عليه مثلا 5 , 25 , 50 , 125 , ...
كما في المثال الثاني من الأمثلة التي لدينا
وهو
1234\25
هنا نلاحظ ان 25 يمكن ان نجعلها 100 بالضرب في 4
اذا نقوم بضرب البسط والمقام في 4
(1234×4)\(25×4) = 4936\100 = 49.36
نأخذ مثال آخر للتوضيح
605\50 = (605×2)\(50×2) = 1210\100 = 12.10
3/القسمة بالتبسيط :
أي نستمر في قسمة كل من البسط والمقام على عدد ما حتى نصل إلى أبسط صور لهذا الكسر
كما في المثال الثالث لدينا
432\36
نقسم كل من البسط والمقام على 2
216\18
نكرر العملية
108\9
نقسم كل من البسط والمقام على 3
36\3
نكرر العملية
12\1
وهو الناتج النهائي
4/ القسمة بالتقريب ====> تستعمل فقط مع الاسئلة الاختيارية
مثاال
100009\100
نلاحظ ان الـ(9) لن تؤثر كثيرا في الناتج النهائي
لذلك نطرحها من العدد
100009 - 9 = 100000
ونقوم بالقسمة الان
100000\100 = 1000
مع العلم ان الناتج الاصلي هو 1000.09
نلاحظ انه لا يوجد فرق كبير بينهما
5/طريقة تجزيء العدد إلى أعدد مجموعة لتسهيل القسمة أو الضرب :
وهي الطريقة التي أستعملها دائما
مثال
494949\49
العدد 494949 يمكن تقسيمه الى 490000 + 4900 + 49
الان نقوم بالقسمة
(490000 + 4900 + 49)\ 49
= (490000\49) + (4900\49) + (49\49)
= 10000 + 100 + 1 = 10101
ونلاحظ أنه نفس الناتج الذي حصلنا عليه بالقسمة المطولة ولكن بطريقة أسهل
مثال آخر
432\36
الان كيف نقسم العدد 432 الى أجزاء بحيث نسهل القسمة على 36
نضرب36 × 10 = 360
نطرح الـ(360) من الـ(432)
432 - 360 = 72
وبكذ نكون حصلنا على قسمين يسهل قسمتهم على 36
الان نقوم بالقسمة
(360 + 72)\36
=(360\36) + (72\36)
= 10 + 2 = 12
نلاحظ أنه نفس الناتج ولكن بطريقة أبسط بكثييير
الآن نأخذ مثال على الضرب
1234 × 4
نجزأ العدد 1234 الى
1000 + 200 + 30 + 4 ونقوم بالضرب
4×(1000 + 200 + 30 +4)
=(4×1000) + (4×200) + (4×30) + (4×4)
= 4000 + 800 + 120 + 16 = 4936
وصدقوني الطريقة الأخيرة دي مفييدة جدا وسهلت عليا القسمة والضرب كثيييرا
منقووووووووووووووول للفائدة