مہجہرد إنہسہآن
ادارة الموقع
الأهداف الفرعية التي يمكن تحقيقها :
1- التعرف على الكسر والمفاهيم المتعلقة به
2- التعرف على تمثيل الكسور
3- التعرض لمفهوم التقاطع ( بين الصفوف والأعمدة )
4- حساب ناتج ضرب كسرين
5- التعرف على كسور الوحدة
شرح البرنامج
اسم البرنامج : تمثيل ضرب كسرين
المثال الأول (1) : ضرب الكسور
مثال : مثل بالرسم :
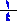
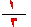
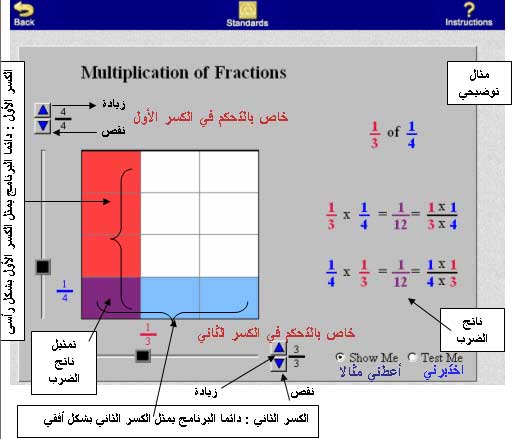
يرينا المثال أعلاه حاصل ضرب كسرين هما
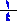
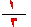
1- يمثل الكسر الأول رأسيا ويمكن التحكم بالأسهم الخاصة به زيادة أو نقصا في البسط . ( التمثيل باللون الأحمر )
2- يمثل الكسر الثاني أفقيا ويمكن التحكم بالأسهم الخاصة به زيادة أو نقصا في البسط . ( التمثيل باللون الأزرق )
3- منطقة التقاطع بين الأعمدة والصفوف المشتركة تمثل ناتج الضرب ( التقاطع هنا في مربع واحد باللون البنفسجي من 12 مربع موجودة في الرسم وعليه فناتج الضرب هو
لمثال 2 : أوجد ناتج ضرب :
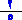
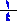
ونريد تمثيل ناتج الضرب للكسرين ، ويكون التمثيل كما يلي :
1- من الأيقونة رقم (1) المُشار إليها نحاول جعل المقام خمسة وعندها يتكون في الرسم صفوف خمسة .
2- من الأيقونة رقم (2) المُشار إليها نحاول جعل البسط = 2 عندها نحصل على صفين مظللين باللون السماوي .
3- من الأيقونة رقم (3) المُشار إليها نحاول جعل المقام أربعة وعندها يتكون في الرسم أربعة أعمدة .
4- من الأيقونة رقم (4) المُشار إليها نحاول جعل البسط = 1 عندها نحصل على عمود واحد مظلل باللون الأحمر .
5- بالنظر إلى الشكل أدناه : لدينا 20 ( عشرون ) مربعا ظللنا منها 2 ( مربعان ) ظللا باللون البنفسجي وهما المربعان الممثلان لتقاطع الصفوف السماوية اللون مع العمود الأحمر اللون . عندها نقول أن المربعين المشار إليهما في الأيقونة رقم (5) هما المربعان الممثلان لناتج الضرب المساوي
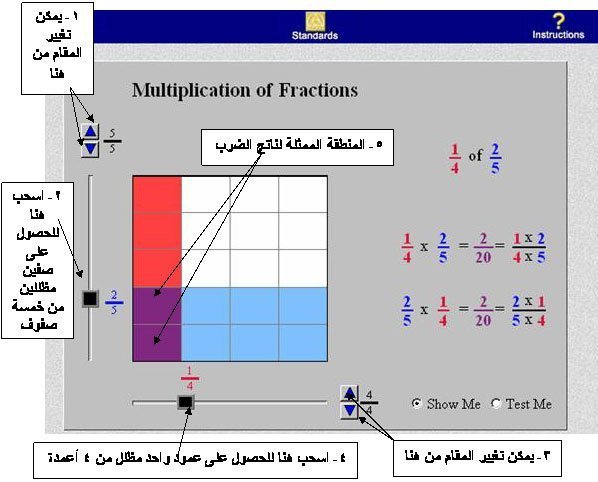
ختاما نستطيع تلخيص الحل بقولنا :
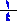
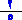
( نظلل 2 منها ) ، وأربعة أعمدة ( نظلل أحدها ) . وعليه نحصل على عشرون مربعا في الجدول .
المنطقة التي تمثل تقاطع الصوف والأعمدة = مربعين من 20 مربعا هي ناتج الضرب
المثال 3 : أوجد ناتج ضرب :
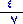
ونريد تمثيل ناتج الضرب للكسرين ، ويكون التمثيل كما يلي :
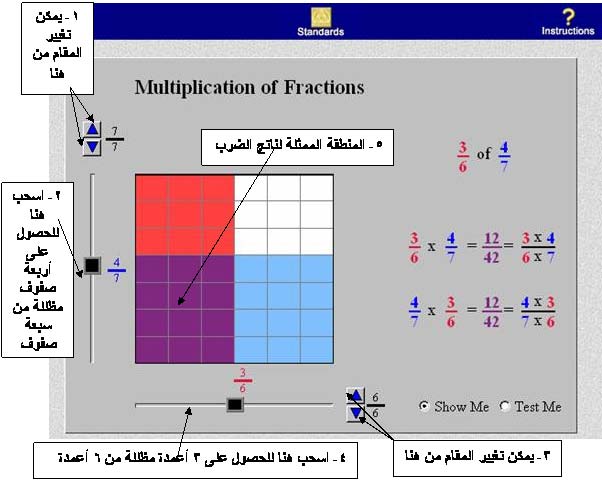
1- من الأيقونة رقم (1) المُشار إليها نحاول جعل المقام سبعة وعندها يتكون في الرسم صفوف سبعة .
2- من الأيقونة رقم (2) المُشار إليها نحاول جعل البسط = 4 عندها نحصل على 4 صفوف مظللة باللون السماوي .
3- من الأيقونة رقم (3) المُشار إليها نحاول جعل المقام ستة وعندها يتكون في الرسم ستة أعمدة .
4- من الأيقونة رقم (4) المُشار إليها نحاول جعل البسط = 3 عندها نحصل على 3 أعمدة مظللة باللون الأحمر .
5- بالنظر إلى الشكل أدناه : لدينا 42 ( اثنان وأربعون ) مربعا ظللنا منها 12 ( اثنا عشر مربعا ) باللون البنفسجي وهي المربعات الممثلة لتقاطع الصفوف السماوية اللون مع الأعمدة الحمراء اللون . عندها نقول أن المربعات المشار إليهما في الأيقونة رقم (5) هما المربعات الممثلة لناتج الضرب
ختاما نستطيع تلخيص الحل بقولنا :
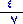
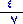
( نظلل 4 منها ) ، وستة أعمدة ( نظلل 3 منها ) . وعليه نحصل على 42 مربعا في الجدول .
المنطقة التي تمثل تقاطع الصوف والأعمدة = 12 مربعا من 42 هي ناتج الضرب ويساوي
