مہجہرد إنہسہآن
ادارة الموقع
-
- إنضم
- 27 أغسطس 2009
-
- المشاركات
- 40,634
-
- مستوى التفاعل
- 1,619
-
- النقاط
- 113
-
- العمر
- 43
-
- الإقامة
- الطفيلة الهاشمية
الأعداد التخيلية " المركبة "
أن مجموعة الأعداد المركبة أوجدت نتيجة للتوسع الطبيعي لمجموعة الأعداد الحقيقية ، مثلما كانت مجموعة الأعداد الحقيقية توسع طبيعي لمجموعة الأعداد القياسية ( النسبية ) وهكذا .
من اخترع أو ابتكر العدد المركب: أن الرياضيين تعاملوا مع هذا العدد أول مرة خلال القرن السادس عشر الميلادي ، وبعد قرنين توسع التعامل معه على أيدي رياضيين مثل أويلر وبرنولي و ديموافر ، واستخدمت الأعداد المركبة في هذه الفترة في تطبيقات مهمة مثل الجبر ونظرية المعادلات وفي حساب التفاضل والتكامل والهندسة ، وأول من وضع له أساس منطقي فهو : جاوس وهاملتون .

أهمية الأعداد المركبة : الأعداد العقدية أو المركبة ذات أهمية لا يمكن تصورها و خصوصاً في مجال الهندسة الالكترونية و الاتصالات حيث أنه في الكثير من المواضيع الهندسية لدينا نمثل المقادير الكهربائية بشكل عقدي و نحصل نتيجة لذلك على حسابات سهلة لمواضيع معقدة بالأساليب العادية
إن أهمية الأعداد المركبة أمر أكبر أن تناقش هنا , وتطبيقاته في الفيزياء والفلك وغيرها أكثر من أن تحصر , أما في الرياضيات نفسها فإن أي معادلة جبرية من الدرجة ن لها ن من الجذور في المستوى المركب (قد يكون بعضها مكررا ) في حين أن عددا غير منته من المعادلات الجبرية ليس لها حل في مجموعة الأعداد الحقيقية .

تظهر الأعداد المركبة في دراسة الظواهر الفيزيائية بشكل غير متوقع
مثلا هناك العديد من المعادلات التفاضلية اللتي تمثل:
- كيفية عمل الدارة الكهربية: الرفاص المضغوط كسيارة تمر فوق أحد المطبات يمكن تمثيل حركة ممتص الصدمات بواسطة معادلة تفاضلية تحتوي علئ أعداد مركبة

- في الفيزياء الكمية لا يمكن تحديد موقع ذرة بدقة بدون الأعداد المركبة:

- حركة دوران الكواكب ( دوائر تتحرك داخل دوائر اخرى )

- في الهندسة : إيجاد طول قطر الخماسي

- لحل بعض التكاملات الحقيقية
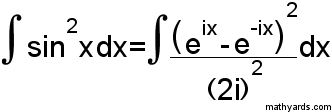
- لتبسيط متسلسلة فورير

(( بالمرفق لغز رياضي يبين أهمية الأعداد التخيلية ))
- مثال رياضي : ما هو الجذر المليون للعدد 1 في الاعداد الحقيقية؟ إنه العدد1 فقط بينما لو بحثنا عن الجذر المليون للعدد 1 في الأعداد المركبة لوجدنا مليون جذر مركب مختلف . أليست هذه المجموعة من الأعداد تستحق التقدير؟؟
- و كمثال من نوع آخر في المعادلات التفاضلية من الدرجة الثانية مثلاً مثل حالة اهتزاز نابض مع كتلة .. فإن حلول المعادلات الأولية تكون عبارة عن مجموع لمقادير عقدية أسية ذات أساس نيبري e و لكن عند الوصول للحل النهائي تزول القيم التخيلية (تختصر) و يظهر الحل مثلاً على أنه اهتزاز جيبي متخامد

فلو توقف الشخص عن حل المعادلة المميزة من الدرجة الثانية كون المميز سالباً لا جذر له فيصل إلى العجز عن الحل ..
الموضوع طويل و التطبيقات كثيرة مثلاً في التحكم الآلي

مثال فيزيائي ( سرعة الألكترونات ) واستخدام الأعداد التخيلية :
استطاع الإنسان في سياق تقدمه وارتقائه أن يحصل على سرعة مناسبة لكل السرعات الأعلى للسيارات والطائرات عندما برزت الحاجة للانتقال على كامل الكرة الأرضية، واليوم يبدأ الإنسان رحلته الكونية، إن سرعة الآلات بل وسرعة الضوء لا تكفي أبداً، فالوصول مثلاً إلى مركز المجرة بسرعة الضوء يستغرق ثلاثين ألف سنة، هل يستطيع الإنسان تجاوز سرعة الضوء لتأمين رحلاته الكونية، كما تجاوز السرعات البطيئة في مسيرته الحياتية على كوكب الأرض، إن كان للصلات الاجتماعية الحياتية الكونية أن تتحقق فلا بد من تجاوز سرعة الضوء، ترتبط السرعة بالكتلة، إن الأجسام ذوات الكتل المقاسة لا تستطيع أن تتسارع إلى سرعة الضوء، تحقق الفوتونات وهي جسيمات المجال الكهرمغنطيسي هذه الخاصية، يقول الفيزيائيون إن الكتلة السكونية للفوتون تطابق الصفر، كيف يمكن أن نمضي في نفس السياق باحثين عن سرعات أعلى من سرعة الضوء، تسعفنا وكما هي العادة وعلى الدوام الرياضيات، تقدم لنا الرياضيات الأعداد التخيلية، إذا أقحمنا الأعداد التخيلية في نظرية النسبية نحصل على جسيمات لا تتحرك إلا بسرعات أكبر من سرعة الضوء، إنها جسيمات عجيبة، إذا خفضنا من طاقاتها تزداد سرعتها، وإذا زودناها بشكل مطرد بالطاقة تتناقص سرعاتها، إذا توفرت لهذه الجسيمات طاقات لانهائية لها فإن سرعاتها تنخفض إلى سرعة الضوء، لكن يستحيل أن تنخفض دونها، دعا العلماء هذه الجسيمات التي مازالت جسيمات افتراضية حتى اللحظة التاشيونات والكلمة من أصل يوناني وتعني السريع، إنها افتراضية بمعنى أن العلماء لم يلتقطوا حتى الآن وبشكل عملي تاشيوناً واحداً.

أن مجموعة الأعداد المركبة أوجدت نتيجة للتوسع الطبيعي لمجموعة الأعداد الحقيقية ، مثلما كانت مجموعة الأعداد الحقيقية توسع طبيعي لمجموعة الأعداد القياسية ( النسبية ) وهكذا .
من اخترع أو ابتكر العدد المركب: أن الرياضيين تعاملوا مع هذا العدد أول مرة خلال القرن السادس عشر الميلادي ، وبعد قرنين توسع التعامل معه على أيدي رياضيين مثل أويلر وبرنولي و ديموافر ، واستخدمت الأعداد المركبة في هذه الفترة في تطبيقات مهمة مثل الجبر ونظرية المعادلات وفي حساب التفاضل والتكامل والهندسة ، وأول من وضع له أساس منطقي فهو : جاوس وهاملتون .

أهمية الأعداد المركبة : الأعداد العقدية أو المركبة ذات أهمية لا يمكن تصورها و خصوصاً في مجال الهندسة الالكترونية و الاتصالات حيث أنه في الكثير من المواضيع الهندسية لدينا نمثل المقادير الكهربائية بشكل عقدي و نحصل نتيجة لذلك على حسابات سهلة لمواضيع معقدة بالأساليب العادية
إن أهمية الأعداد المركبة أمر أكبر أن تناقش هنا , وتطبيقاته في الفيزياء والفلك وغيرها أكثر من أن تحصر , أما في الرياضيات نفسها فإن أي معادلة جبرية من الدرجة ن لها ن من الجذور في المستوى المركب (قد يكون بعضها مكررا ) في حين أن عددا غير منته من المعادلات الجبرية ليس لها حل في مجموعة الأعداد الحقيقية .

تظهر الأعداد المركبة في دراسة الظواهر الفيزيائية بشكل غير متوقع
مثلا هناك العديد من المعادلات التفاضلية اللتي تمثل:
- كيفية عمل الدارة الكهربية: الرفاص المضغوط كسيارة تمر فوق أحد المطبات يمكن تمثيل حركة ممتص الصدمات بواسطة معادلة تفاضلية تحتوي علئ أعداد مركبة

- في الفيزياء الكمية لا يمكن تحديد موقع ذرة بدقة بدون الأعداد المركبة:

- حركة دوران الكواكب ( دوائر تتحرك داخل دوائر اخرى )

- في الهندسة : إيجاد طول قطر الخماسي

- لحل بعض التكاملات الحقيقية
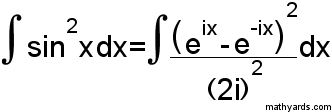
- لتبسيط متسلسلة فورير

(( بالمرفق لغز رياضي يبين أهمية الأعداد التخيلية ))
- مثال رياضي : ما هو الجذر المليون للعدد 1 في الاعداد الحقيقية؟ إنه العدد1 فقط بينما لو بحثنا عن الجذر المليون للعدد 1 في الأعداد المركبة لوجدنا مليون جذر مركب مختلف . أليست هذه المجموعة من الأعداد تستحق التقدير؟؟
- و كمثال من نوع آخر في المعادلات التفاضلية من الدرجة الثانية مثلاً مثل حالة اهتزاز نابض مع كتلة .. فإن حلول المعادلات الأولية تكون عبارة عن مجموع لمقادير عقدية أسية ذات أساس نيبري e و لكن عند الوصول للحل النهائي تزول القيم التخيلية (تختصر) و يظهر الحل مثلاً على أنه اهتزاز جيبي متخامد

فلو توقف الشخص عن حل المعادلة المميزة من الدرجة الثانية كون المميز سالباً لا جذر له فيصل إلى العجز عن الحل ..
الموضوع طويل و التطبيقات كثيرة مثلاً في التحكم الآلي

مثال فيزيائي ( سرعة الألكترونات ) واستخدام الأعداد التخيلية :
استطاع الإنسان في سياق تقدمه وارتقائه أن يحصل على سرعة مناسبة لكل السرعات الأعلى للسيارات والطائرات عندما برزت الحاجة للانتقال على كامل الكرة الأرضية، واليوم يبدأ الإنسان رحلته الكونية، إن سرعة الآلات بل وسرعة الضوء لا تكفي أبداً، فالوصول مثلاً إلى مركز المجرة بسرعة الضوء يستغرق ثلاثين ألف سنة، هل يستطيع الإنسان تجاوز سرعة الضوء لتأمين رحلاته الكونية، كما تجاوز السرعات البطيئة في مسيرته الحياتية على كوكب الأرض، إن كان للصلات الاجتماعية الحياتية الكونية أن تتحقق فلا بد من تجاوز سرعة الضوء، ترتبط السرعة بالكتلة، إن الأجسام ذوات الكتل المقاسة لا تستطيع أن تتسارع إلى سرعة الضوء، تحقق الفوتونات وهي جسيمات المجال الكهرمغنطيسي هذه الخاصية، يقول الفيزيائيون إن الكتلة السكونية للفوتون تطابق الصفر، كيف يمكن أن نمضي في نفس السياق باحثين عن سرعات أعلى من سرعة الضوء، تسعفنا وكما هي العادة وعلى الدوام الرياضيات، تقدم لنا الرياضيات الأعداد التخيلية، إذا أقحمنا الأعداد التخيلية في نظرية النسبية نحصل على جسيمات لا تتحرك إلا بسرعات أكبر من سرعة الضوء، إنها جسيمات عجيبة، إذا خفضنا من طاقاتها تزداد سرعتها، وإذا زودناها بشكل مطرد بالطاقة تتناقص سرعاتها، إذا توفرت لهذه الجسيمات طاقات لانهائية لها فإن سرعاتها تنخفض إلى سرعة الضوء، لكن يستحيل أن تنخفض دونها، دعا العلماء هذه الجسيمات التي مازالت جسيمات افتراضية حتى اللحظة التاشيونات والكلمة من أصل يوناني وتعني السريع، إنها افتراضية بمعنى أن العلماء لم يلتقطوا حتى الآن وبشكل عملي تاشيوناً واحداً.
