مہجہرد إنہسہآن
ادارة الموقع
وحدات البناء الاساسية
1- الفئة Set : هى عبارة عن ثُلة collection من الاشياء التى ليس من الضروري ان يربط بينها رابط مشترك او تحقق اى خواص اضافية فمثلاً ثُلة من n شخص تمثل فئة من الاشخاص و كذلك ايضاً ثُلة من n نقطة تمثل فئة من النقاط. و عدد العتاصر n فى الفئة يمكن ان يكون منتهياً او لانهائياً.
.................................................. .................................................. ...........................
2-الزمرة Group :
نقول ان G تمثل زمرة اذا كان لدينا:
a- فئة من العناصر تنتمي للزمرة
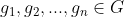
b-عملية ثنائية
تسمى بعملية الضرب على الزمرة
وتحققت الشروط :
A1- الاغلاق Closure
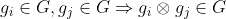
A2-العملية التجميعية Associativity
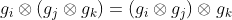
A3-وجود عنصر محايد
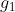
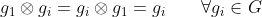
A4- وجود معكوس وحيد
لكل عنصر
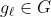يوجد معكوس وحيد
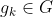يرمز له بـ
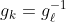و بحيث
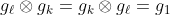
مثال(1):
فئة كل التبديلات الممكنة للنقاط 1, 2 , 3 تشكل زمرة تسمى بزمرة التباديل
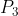
لاحظ ان العنصر المحايد هو عملية عدم اجراء التبديل اى ان النقطة 1 تتحول لمكان النقطة 1 والنقطة 2 تتحول الى مكان النقطة 2 و اخيراً النقطة 3 تتحول الى مكان النقطة 3
اذن قبل اجراء التبديل كل لدينا الترتيب (123) وبعد التبديل اصبح لدينا الترتيب (123) و بالطبع فان هذا التأثير يمثل العنصر المحايد ونرمز له بـ
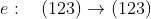
يمكن تبديل النقطتين 1 و 2 وترك النقطة 3 فى مكانها اى ان النقطة 1 تتحول الى النقطة 2 و النقطة 2 تتحول الى النقطة 1 و النقطة 3 تتحول الى النقطة 3
اذن قبل اجراء التبديل كان لدينا الترتيب (123) و بعد التبديل اصبح لدينا الترتيب (213) وهذا العنصر يرمز له بـ
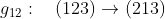
يمكن تثبيت النقطة 2 و تبديل النقاط 1 و 3 و هذا العنصر يرمز له بـ
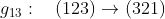
ويمكن ايضاً تثبيت النقطة 1 و تبديل النقاط 2و 3 و هذا العنصر يرمز له بـ
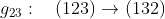
يمكن تبديل جميع النقاط بحيت تتحول اى نقطة الى مكان النقطة التالية فى الترتيب اى تتحول النقطة 1 الى النقطة 2 و تتحول النقطة 2 الى النقطة 3 و تتحول النقطة 3 الى النقطة 1
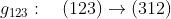
و اخيراً تبديل جميع النقاط بحيث ان اى نقطة تتحول الى مكان النقطة السابقة لها فى الترتيب فمثلاً النقطة 3 تتحول الى النقطة 2 و النقطة 2 تتحول الى النقطة 1 و النقطة 1 تتحول الى النقطة 3 اى ان
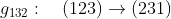
هل يمكن اضافة عنصر آخر؟
اوجد حاصل الضرب
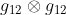. ما الذى يمكن استنتاجه؟
اوجد حاصل الضرب
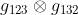. ماذا تستنتج؟
ماذا تتوقع ان يكون عدد عناصر زمرة التبديل
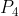
مثال(2):
فئة الاعداد الحقيقية تشكل زمرة تحت عملية الجمع الاعتيادي +
العنصر المحايد هو الـ0
لكل عدد حقيقي a يوجد عدد وحيد حقيقي a- يمثل معكوسه الجمعي
مثال(3) فئة الاعداد الحقيقة باسثناء الـ 0 تشكل زمرة تحت عملية الضرب الاعتيادي
العنصر المحايد هو الـ 1
لكل عنصر a يوجد عنصر وحيد
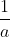يمثل المعكوس الضربي
سؤال: لماذا تم استبعاد الـ 0 ؟
مثال(4):
فئة كل المصفوفات الحقيقية المربعة
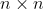الغير شاذة
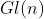تشكل زمرة تحت عملية ضرب المصفوفات
العنصر المحايد هو مصفوفة الوحدة
طالما ان هذه المصفوفات غير شاذة فان لكل مصفوفة يوجد معكوس
فى الزمر التى فى الامثلة 2 و 3 نجد ان الترتيب الذى نجري به العملية الثنائية غير مهم و لذلك نقول انها زمر ابدالية
A5- الخاصية التبادلية commutativity: اذا حققت الزمرة الخاصية
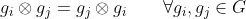
فاننا نقول ان الزمرة G زمرة ابدالية Abelian
ومن الواضح ان الزمر فى الامثلة 1 و 4 هى زمر غير ابدالية (تأكد منها بنفسك)
الحقل F هو
a- الفئة
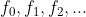
b- وعمليتين هما الجمع (+) والضرب (.)
التى تحقق الشروط التالية
A- الفئة F عبارة عن زمرة ابدالية تحت عملية الجمع + عنصرها المحايد هو
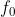اى انها تحققالشروط A1-5
B1- خاصية الاغلاق
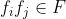
B2- الخاصية التجميعية
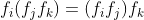
B3- العنصر المحايد
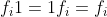
B4- لكل عنصر باستثناء
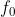يوجد معكوس
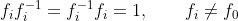
B5- قانون التوزيع Distribution law
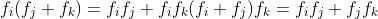
مثال(5):
الاعداد الحقيقية تشكل حقل يسمى بحقل الاعداد الحقيقية
(تأكد من تحقق شروط الحقل )
مثال(6):
الاعداد المركبة يمكن كتابتها بالصورة
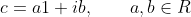بحيث ان
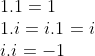
تشكل حقل يسمى بحقل الاعداد المركبة
(تأكد من تحقق شروط الحقل )
مثال (7):
الكوتيريونات Quaternions يمكن تمثيلها بالصورة
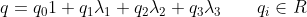
بحيث ان
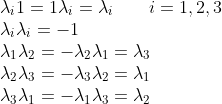
تمرين:
برهن ان الكواتيريونات تشكل حقلاً.
اذا حقق الحقل الخاصية التالية فاننا نقول عنه حقل ابدالي
B6-الخاصية التبادلية
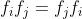
سؤال: هل يعتبر الحقل الكواتيريوني حقلاً ابدالية ؟
1- الفئة Set : هى عبارة عن ثُلة collection من الاشياء التى ليس من الضروري ان يربط بينها رابط مشترك او تحقق اى خواص اضافية فمثلاً ثُلة من n شخص تمثل فئة من الاشخاص و كذلك ايضاً ثُلة من n نقطة تمثل فئة من النقاط. و عدد العتاصر n فى الفئة يمكن ان يكون منتهياً او لانهائياً.
.................................................. .................................................. ...........................
2-الزمرة Group :
نقول ان G تمثل زمرة اذا كان لدينا:
a- فئة من العناصر تنتمي للزمرة
b-عملية ثنائية
وتحققت الشروط :
A1- الاغلاق Closure
A2-العملية التجميعية Associativity
A3-وجود عنصر محايد
A4- وجود معكوس وحيد
لكل عنصر
مثال(1):
فئة كل التبديلات الممكنة للنقاط 1, 2 , 3 تشكل زمرة تسمى بزمرة التباديل
لاحظ ان العنصر المحايد هو عملية عدم اجراء التبديل اى ان النقطة 1 تتحول لمكان النقطة 1 والنقطة 2 تتحول الى مكان النقطة 2 و اخيراً النقطة 3 تتحول الى مكان النقطة 3
اذن قبل اجراء التبديل كل لدينا الترتيب (123) وبعد التبديل اصبح لدينا الترتيب (123) و بالطبع فان هذا التأثير يمثل العنصر المحايد ونرمز له بـ
يمكن تبديل النقطتين 1 و 2 وترك النقطة 3 فى مكانها اى ان النقطة 1 تتحول الى النقطة 2 و النقطة 2 تتحول الى النقطة 1 و النقطة 3 تتحول الى النقطة 3
اذن قبل اجراء التبديل كان لدينا الترتيب (123) و بعد التبديل اصبح لدينا الترتيب (213) وهذا العنصر يرمز له بـ
يمكن تثبيت النقطة 2 و تبديل النقاط 1 و 3 و هذا العنصر يرمز له بـ
ويمكن ايضاً تثبيت النقطة 1 و تبديل النقاط 2و 3 و هذا العنصر يرمز له بـ
يمكن تبديل جميع النقاط بحيت تتحول اى نقطة الى مكان النقطة التالية فى الترتيب اى تتحول النقطة 1 الى النقطة 2 و تتحول النقطة 2 الى النقطة 3 و تتحول النقطة 3 الى النقطة 1
و اخيراً تبديل جميع النقاط بحيث ان اى نقطة تتحول الى مكان النقطة السابقة لها فى الترتيب فمثلاً النقطة 3 تتحول الى النقطة 2 و النقطة 2 تتحول الى النقطة 1 و النقطة 1 تتحول الى النقطة 3 اى ان
هل يمكن اضافة عنصر آخر؟
اوجد حاصل الضرب
اوجد حاصل الضرب
ماذا تتوقع ان يكون عدد عناصر زمرة التبديل
مثال(2):
فئة الاعداد الحقيقية تشكل زمرة تحت عملية الجمع الاعتيادي +
العنصر المحايد هو الـ0
لكل عدد حقيقي a يوجد عدد وحيد حقيقي a- يمثل معكوسه الجمعي
مثال(3) فئة الاعداد الحقيقة باسثناء الـ 0 تشكل زمرة تحت عملية الضرب الاعتيادي
العنصر المحايد هو الـ 1
لكل عنصر a يوجد عنصر وحيد
سؤال: لماذا تم استبعاد الـ 0 ؟
مثال(4):
فئة كل المصفوفات الحقيقية المربعة
العنصر المحايد هو مصفوفة الوحدة
طالما ان هذه المصفوفات غير شاذة فان لكل مصفوفة يوجد معكوس
فى الزمر التى فى الامثلة 2 و 3 نجد ان الترتيب الذى نجري به العملية الثنائية غير مهم و لذلك نقول انها زمر ابدالية
A5- الخاصية التبادلية commutativity: اذا حققت الزمرة الخاصية
فاننا نقول ان الزمرة G زمرة ابدالية Abelian
ومن الواضح ان الزمر فى الامثلة 1 و 4 هى زمر غير ابدالية (تأكد منها بنفسك)
الحقل F هو
a- الفئة
b- وعمليتين هما الجمع (+) والضرب (.)
التى تحقق الشروط التالية
A- الفئة F عبارة عن زمرة ابدالية تحت عملية الجمع + عنصرها المحايد هو
B1- خاصية الاغلاق
B2- الخاصية التجميعية
B3- العنصر المحايد
B4- لكل عنصر باستثناء
B5- قانون التوزيع Distribution law
مثال(5):
الاعداد الحقيقية تشكل حقل يسمى بحقل الاعداد الحقيقية
(تأكد من تحقق شروط الحقل )
مثال(6):
الاعداد المركبة يمكن كتابتها بالصورة
تشكل حقل يسمى بحقل الاعداد المركبة
(تأكد من تحقق شروط الحقل )
مثال (7):
الكوتيريونات Quaternions يمكن تمثيلها بالصورة
بحيث ان
تمرين:
برهن ان الكواتيريونات تشكل حقلاً.
اذا حقق الحقل الخاصية التالية فاننا نقول عنه حقل ابدالي
B6-الخاصية التبادلية
سؤال: هل يعتبر الحقل الكواتيريوني حقلاً ابدالية ؟